Carbonation and the Urey reaction k Louise H. KeLLogg1, HarsHa LoKavarapu2, and donaLd L. TurcoTTe2,*,† 1Department of Earth and Planetary Science, University of California, Davis, 1 Shields Avenue, Davis, California 95616, U.S.A.
2Department of Earth and Planetary Science, University of California, Davis, 1 Shields Avenue, Davis, California 95616, U.S.A

摘要

目前地球上有三个主要的碳储存库：地核、地幔和大陆地壳。大陆地壳中的碳主要以碳酸盐形式存在（如石灰岩、大理石等）。本文探讨了碳酸盐的来源。1952年，哈罗德·尤里提出，由侵蚀作用产生的钙硅酸盐与大气中的二氧化碳反应生成碳酸盐，这一反应现被称为尤里反应。本文首先讨论了尤里反应如何从早期的大气中清除大量地壳碳。当前，尤里反应主导着大气中二氧化碳的浓度。二氧化碳通过火山活动进入大气，并通过尤里反应被转移到大陆地壳。我们将详细探讨这一过程。接下来，我们讨论了古新世—始新世温度极大期（PETM）的衰减过程。我们定量分析了尤里反应如何消除大气中注入的二氧化碳。典型的衰减时间为10万年，但这一过程的时间取决于尤里反应的速率变化。

引言

大陆地壳是地球上碳的主要储存库之一。地质学中的一个重要问题是碳的来源，主要以钙碳酸盐的形式存在。解释大陆地壳中钙碳酸盐（如石灰岩、大理石）来源的首次成功尝试是由尤里（Urey，1952年）提出的。他给出的基本方程式为：

$$ \text{CaSiO}_3 + \text{CO}_2 \rightleftharpoons \text{CaCO}_3 + \text{SiO}_2 $$

他提出，大气中的二氧化碳与钙硅酸盐反应，生成钙碳酸盐和二氧化硅。他在论文中直接引用道：“随着二氧化碳的形成，它与硅酸盐反应形成石灰岩。当然，硅酸盐可能是多种矿物，但通过这一反应或类似的反应，大气中的二氧化碳始终保持在较低水平，就像现在一样。”

在当前的文献中，尤里反应的扩展版本被给出（Blättler 和 Higgins，2017年）。为了包括酸雨的作用，尤里反应可以写成：

$$ \text{CaSiO}_3 + 2\text{CO}_2 + \text{H}_2\text{O} \rightarrow \text{Ca}^{2+} + 2\text{HCO}_3^{-} + \text{SiO}_2 \quad \rightarrow \quad \text{CaCO}_3 + \text{SiO}_2 + \text{CO}_2 + \text{H}_2\text{O} $$

碳酸盐化反应发生在酸雨中的二氧化碳（碳酸）溶解钙硅酸盐（如透闪石）沉积物时，生成钙、碳酸氢根和二氧化硅。生成的钙和碳酸氢根离子通过河流流入海洋，在那里，生物或无机沉淀作用生成钙碳酸盐。

地球碳的储存和循环

目前地球上有三个主要的碳储存库：地核、地幔和大陆地壳。我们假设地核是一个独立的储存库，忽略它的作用。地球上约有1%的碳存在于大陆地壳中。Wedepohl（1995年）对大陆地壳的成分进行了全面研究，重点讨论了碳的含量。他估算了当前大陆地壳中碳的总质量（c），为：

$$ cM_{\text{ccp}} = 4.2 \times 10^7 \, \text{Gt} $$

Hayes 和 Waldbauer（2006年）回顾了有关大陆地壳中碳的文献，并建议其质量可能高达：

$$ cM_{\text{ccp}} = 10^8 \, \text{Gt} $$

DePaolo（2015年）给出了6到7 × 10^7 Gt的范围。在本文中，我们取一个代表性值：

$$ cM_{\text{ccp}} = 5 \times 10^7 \, \text{Gt} $$

海洋中的碳质量大约是大陆地壳中碳质量的千分之一（Houghton，2007年）。

尤里反应对大气二氧化碳的影响

尤里（1952年，1956年）明确认识到他提出的反应将有效地从地球的大气中去除二氧化碳，但当时对于早期大气的了解很少。尽管当前大气中碳的质量较小（850 Gt），但过去的碳质量可能远高于此。

金星和地球之间的主要区别之一是大气成分。金星的大气压大约是地球的大气压的100倍，且其大气中96%为二氧化碳。金星大气中的碳质量（\( c \)）为：

$$ cM_{\text{ap}} = 1.28 \times 10^8 \, \text{Gt} $$

将金星和地球的大气碳质量与总体质量进行缩放，可以估算出地球早期大气中的碳质量（\( t = 0 \)）。估算值为：

$$ cM_{\text{a0}} = 1.57 \times 10^8 \, \text{Gt} $$

（Kasting 和 Ackerman，1986年）

碳从大气到大陆地壳的转移

关于大陆地壳中碳的来源，一种假设是碳是在地球历史的早期直接从大气中提取的。上述给出的早期大气中碳的质量（\(cM_a0 = 1.57 \times 10^8 \, \text{Gt}\)）远大于大陆地壳中碳的总质量（\(cM_{\text{ccp}} = 5 \times 10^7 \, \text{Gt}\)）。这种从大气中直接提取的假设已被Kramers（2002年）和Lowe与Tice（2004年）详细讨论过。

基本假设是，大气到大陆地壳的碳质量通量（\(cJ_{a-cc}\)）受钙硅酸盐的可用性控制。为了使尤里反应能够从大气中提取二氧化碳，早期地球必须拥有大陆地壳，从而生成钙硅酸盐的表面沉积物。此外，地球必须拥有海洋，才能使酸雨催化大气二氧化碳与钙硅酸盐沉积物之间的尤里反应。关于二氧化碳从大气中提取的启动时间，几乎没有数据可用。我们假设该过程始于早期撞击和约44亿年前地幔海洋的固化后的一段时间（\(t_0\)）。我们进一步假设，在大气中二氧化碳浓度减少到极低水平之前，尤里反应以恒定速率从大气中提取碳（\(cJ_{a-cc}\)）。在此期间（\(t_0 < t < t_0 + t_{a-cc}\)），尤里反应将大气中的碳提取到大陆地壳。

我们将指定从大气中提取的碳的质量，并得出如下结论：

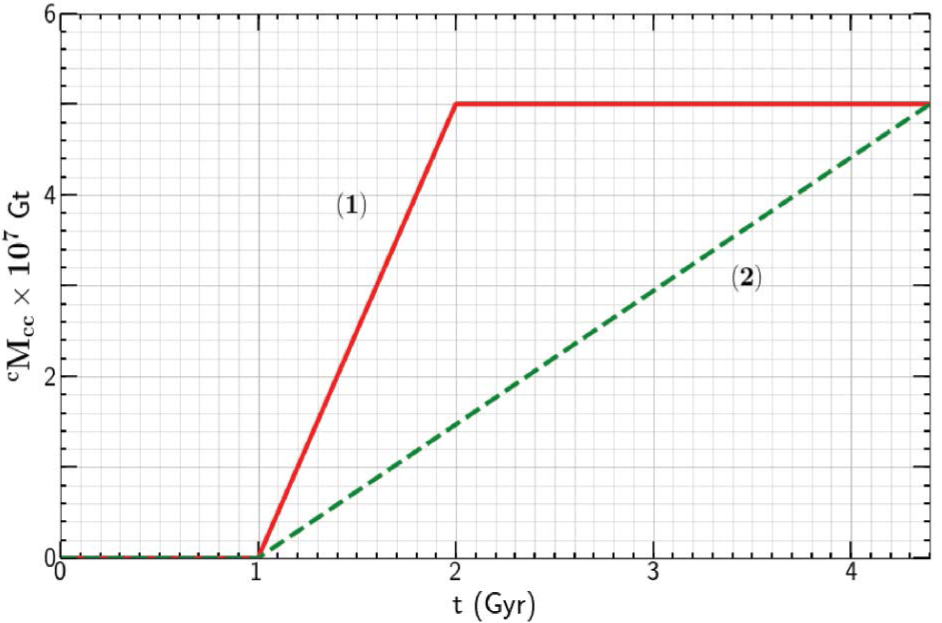
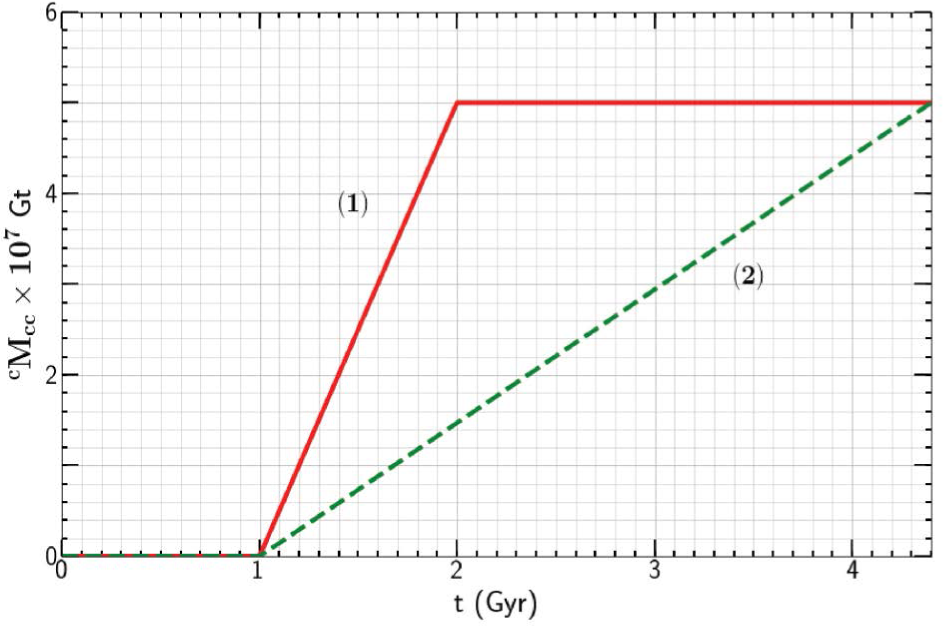
大陆地壳中碳质量 cMcc 对时间的依赖性。给出了两个极限模型，用于添加当前质量 cMccp = 5 × 10⁷ Gt。 （1）从大气中加入，从 t₀ = 1 Gyr。所有大气碳都以恒定通量 cJa-cc = 50 Mtyr^-1 以 τa-cc = 1 Gyr 的形式转移。 （2）从地幔开始添加，从 t₀ = 1 Gyr。碳以恒定通量 cJm-cc = 14.7 Mtyr^-1 添加到现在。

图1：大陆地壳中碳的质量（\(cM_{\text{cc}}\)）随时间的变化

对于添加当前质量（\(cM_{\text{ccp}} = 5 \times 10^7 \, \text{Gt}\)），给出了两种极限模型：

1. 从大气中开始添加，\(t_0 = 1 \, \text{Gyr}\)。所有大气中的碳在\(t_{a-cc} = 1 \, \text{Gyr}\)内以恒定的通量（\(cJ_{a-cc} = 50 \, \text{Mt/yr}\)）转移。
2. 从地幔中开始添加，\(t_0 = 1 \, \text{Gyr}\)。碳以恒定的通量（\(cJ_{m-cc} = 14.7 \, \text{Mt/yr}\)）添加至现在。

我们假设，大气中的碳质量（\(cM_a\)）在时间上呈线性下降，从\(cM_{a0}\)降至零，而大陆地壳中的碳质量则在时间上呈线性增加。

假设大陆地壳中的所有碳（\(cM_{\text{ccp}}\)）都是从大气中提取的，那么碳质量随时间的变化关系为：

$$ cM_{\text{cc}} = 0, \quad 0 \leq t \leq t_0 $$

$$ cM_{\text{cc}} = cM_{\text{ccp}} \left[ \frac{t - t_0}{t_{a-cc}} \right], \quad t_0 \leq t \leq t_0 + t_{a-cc} $$

$$ cM_{\text{cc}} = cM_{\text{ccp}}, \quad t_0 + t_{a-cc} \leq t \leq t_p $$

取\(cM_{\text{ccp}} = 5 \times 10^7 \, \text{Gt}\)，\(t_0 = 1 \, \text{Gyr}\)，以及\(t_{a-cc} = 1 \, \text{Gyr}\)，则\(cM_{\text{cc}}\)与时间\(t\)的关系如图1所示。所需的大气到大陆地壳的碳通量为\(cJ_{a-cc} = 50 \, \text{Mt/yr}\)。需要强调的是，\(t_{a-cc}\)的值存在不确定性，且通量\(cJ_{a-cc}\)的变化在时间上可能会有较大波动。然而，很显然，从大气中提取碳到大陆地壳的过程是在地球历史的早期完成的。

大气中碳的火山注入去除

当大气中的过量碳被尤里反应消耗后，大气中的碳与通过尤里反应提取的碳之间建立了一种近似的稳态平衡。我们用以下关系来近似这一平衡：

$$ cJ_{a-cc} = cM_a $$

其中，\(cJ_{a-cc}\) 是火山注入大气的碳的速率。我们假设这一提取速率是恒定的，并且与大气中的碳质量 \(cM_a\) 成正比。特征时间 \(t_u\) 考虑了酸雨与钙硅酸盐沉积物之间反应的速率，尽管我们假设 \(t_u\) 是常数，但显然它可能是随时间变化的。

Berner 和 Kothavala（2001年）提出了一个关于寒武纪时代以来大气中CO2变动的全面模型。这个模型 GEOCARB III 很复杂，涉及有机和无机过程。在百万年尺度上，模型量化了大气、海洋和大陆地壳之间碳的交换。碳平衡主要受到大陆地壳中的碳酸盐和表面储库（如海洋和大气）之间碳交换的主导作用，此外有机碳也起到重要作用（Berner 和 Caldeira 1997年）。

当侵蚀率高时，尤里反应从大气中提取CO2，增加大陆地壳中的碳酸盐。高侵蚀率通常与低海平面和大面积大陆相关。当侵蚀率低时，尤里反应则在相反方向（方程式1中的右到左）进行，碳酸盐分解释放CO2。这一变质过程的一个例子是碳酸盐沉积物的俯冲作用，以及在俯冲带火山中生成并返回大气中的CO2（Frezzotti et al. 2011年）。

目前大气中的碳质量为860 Gt（400 ppmv CO2），但由于人为活动的高通量注入（3.5 Gt/年），这一值并不是一个准平衡值。我们将1900年的650 Gt（300 ppmv CO2）作为当前的平衡值。这是当前冰川期的典型值（0到5000万年）。GEOCARB III模型给出的数值通常与观察结果一致（Royer 2014年）。在50到250百万年之间，平均值约为3000 Gt。在250到350百万年之间的主要冰川期，观察到的值接近650 Gt。350到550百万年之间的值明显较高，通常接近10000 Gt。这一变动反映了方程3中的两个变量的变化，即火山通量 \(cJ_{a-cc}\) 进入大气和特征时间 \(t_u\)。

来自地幔到大陆地壳的碳

第二种关于大陆地壳中碳来源的假设是碳来自地幔。如果地幔中从洋脊和热点释放的火山碳通量超过了在俯冲带失去的碳量，那么差额将被添加到大陆地壳中。部分火山碳输入将进入大气，并通过尤里反应转移到大陆地壳。然而，一些碳将进入海洋并直接转化为碳酸盐，而不经过大气。

火山作用和通过俯冲带损失的碳的速率肯定会在地质时间尺度上变化，但这些变化尚不明确。我们假设，为了实现碳的转移，地球的板块构造过程始于大约45亿年前的固化的岩浆海洋之后的某一时间 \(t_0\)。我们进一步假设，直到现在为止，碳的地幔转移速率保持恒定 \(cJ_{m-cc}\)。假设大陆地壳中的所有碳都来自地幔，则时间依赖关系由以下公式给出：

$$ cM_{\text{cc}} = 0, \quad 0 \leq t \leq t_0 $$

$$ cM_{\text{cc}} = cM_{\text{ccp}} \left[ \frac{t - t_0}{t_p - t_0} \right], \quad t_0 \leq t \leq t_p $$

在此期间，大陆地壳中的碳质量是线性增长的，所需的碳通量 \(cJ_{m-cc}\) 为：

$$ cJ_{m-cc} = \frac{cM_{\text{ccp}}}{t_p - t_0} $$

假设 \(cM_{\text{ccp}} = 5 \times 10^7 \, \text{Gt}\)，\(t_0 = 1 \, \text{Gyr}\)，以及 \(t_p = 4.4 \, \text{Gyr}\)，则碳的依赖关系如图1所示。所需的地幔到大陆地壳的碳通量为 \(cJ_{m-cc} = 14.7 \, \text{Mt/yr}\)。

当前火山从地幔到大气的碳损失估计

Dasgupta 和 Hirschmann（2010年）总结了有关地幔到表面储库的碳损失的数据，并给出了范围为 \(cJ_{m-s} = 36 \pm 24 \, \text{Mt/yr}\) 的值。正如碳通过火山作用从地幔中损失一样，碳也通过俯冲作用返回地幔。Kelemen 和 Manning（2015年）对俯冲带碳通量进行了详细研究，他们建议全球俯冲带的向下碳通量为 \(53 \pm 13 \, \text{Mt/yr}\)。然而，这一部分碳有相当大的一部分由于俯冲带的火山作用未能到达地幔，他们建议约有 \(24 \pm 24 \, \text{Mt/yr}\) 的碳能到达地幔。

显然，地幔中的所有碳都可能来自地幔。Hayes 和 Waldbauer（2006年）也得出了类似的结论。

在图1中，我们给出了两种极限情况下的示例：大陆地壳中的碳完全来自大气，碳完全来自地幔。在第一种情况下，碳的加入较早；而在第二种情况下，加入更加均匀。通过观察大陆地壳中碳酸盐的质量与年龄的关系，可能能够区分这两种情况，但数据较为稀缺。通过观察大气中碳的质量随时间的变化，也可能为我们提供约束条件。Rye 等人（1995年）通过研究古土壤得出结论：大约在22亿至27.5亿年前，大气中的碳质量小于 \(10^5 \, \text{Gt}\)。这一结论表明，从大气中提取到大陆地壳的大量碳是在大约20亿年前完成的。然而，这一质量的具体大小仍不确定。

古新世—始新世温度极大期（PETM）

古新世—始新世温度极大期（PETM）的衰减可以用来定量限制尤里反应的作用。PETM是一个全球温度升高（4至5°C）和大气CO2浓度升高的时期，始于5630万年前，开始持续不到1万年，随后的衰减持续约10万年（Mclnerney 和 Wing 2011年）。Storey等人（2007年）强烈支持将PETM与北大西洋裂谷引起的大规模火山爆发联系起来。

通过同位素研究，PETM的过程得到了定量记录。这些研究由Gutjahr等人（2017年）回顾过，他们还提供了PETM期间大气中碳的估计值。他们建议，PETM前后的背景大气碳质量为 \(cM_{\text{ab}} = 1400 \, \text{Gt}\)，而碳的峰值质量为 \(cM_{a0} = 3050 \, \text{Gt}\)。

我们现在进行PETM衰减的分析，考虑到尤里反应从大气中去除CO2。我们扩展方程5，加入暂时性的碳去除，并写成：

$$ \frac{dM}{dt} = J_{a-cc} \left( M_a - M_{\text{ab}} \right) - \frac{M_a}{t_u} $$

从方程5可得，大气中碳的背景质量为：

$$ M_{\text{ab}} = J_{a-cc} \left( M_a - M_{\text{ab}} \right) \frac{1}{t_u} $$

我们将初始的大气碳质量 \(cM_{a0}\) 设定为，并解方程7，假设 \(t_u\) 是常数，得到如下结果：

$$ M_a(t) = M_a0 - (M_a0 - M_{\text{ab}}) e^{-t/t_u} $$

大气中碳的过量质量 \(M_{a0} - M_{\text{ab}}\) 随着尤里反应从大气中提取碳而呈指数衰减。

接下来，我们根据方程10的模型依赖关系，获取PETM期间大气中碳质量随时间的变化。取 \(cM_{\text{ab}} = 1400 \, \text{Gt}\) 和 \(cM_{a0} = 3050 \, \text{Gt}\)，并假设 \(t_u = 100 \, \text{kyr}\)，得到的模型结果如图2所示。

讨论

尤里（1952年）提出了尤里反应（方程1），以解释大陆地壳中碳酸盐的来源。他认为这一反应将基本去除大气中的所有二氧化碳。现在普遍认为，与金星类似，地球早期的大气中可能存在大量碳，甚至多达 \(10^8\) Gt。然而，这部分碳在月球形成的撞击事件中可能只幸存了一部分。

我们给出了一个非常简化的模型来解释碳从大气到大陆地壳的提取过程，假设提取速率 \(cJ_{a-cc}\) 是常数。这个速率随时间的变化基本没有约束。如果大陆地壳中的大量碳是从大气中提取的，那么这很可能发生在地球历史的早期，如图1所示。

尤里反应还控制着大气中碳的平衡质量，特别是在去除任何初始大浓度之后。大气中碳的输入来自火山活动，我们表明，大气中碳的平衡质量 \(cM_{\text{ab}}\) 与火山碳注入速率 \(cJ_{a-cc}\) 成正比，并且与特征时间 \(t_u\) 成反比。我们通过研究古新世—始新世温度极大期（PETM）观察到的放松过程，量化了 \(t_u\) 的值，并得出放松时间约为 \(t_u = 10^5 \, \text{年}\)。

我们还给出了一个简化模型，解释了碳从大气到大陆地壳的提取过程。如果地幔中通过火山作用释放的碳损失超过了通过俯冲作用返回地幔的碳量，那么差额将被加入到大陆地壳中。如果火山碳进入海洋，通过有机沉淀形成碳酸盐。如果火山碳进入大气，它将通过尤里反应进入大陆地壳。

目前的地幔碳通量估计足以产生大陆地壳中的所有碳。目前，尚无法量化早期大气和地幔对大陆地壳中碳的贡献相对重要性。

启示

本文我们探讨了关于大气中碳的两个主要问题。第一个问题是大陆地壳中碳的来源。我们得出结论，碳可能来自早期大气或地幔，且这一过程可能持续了更长时间。我们认为，关于大气和大陆地壳中碳浓度随地质时间的变化的研究应当得到高度重视。

第二个问题是关于大气中碳注入后恢复到平衡值的过程。我们通过研究古新世—始新世温度极大期（PETM）对这一过程进行了量化。这对恢复当前人为碳注入到大气中的过程具有明显的启示。我们发现，恢复时间大约为 5 万年。

PETM 异常的大气碳质量值 cMa 对时间 tPETM 相对于异常开始的依赖性。 这些值来自公式 11 中给出的松弛模型，其中 cMab = 1400 Gt 和 cMa0 = 3050 Gt，τu = 100 kyr。

图2：PETM异常期间大气中碳质量随时间变化的依赖关系

图2展示了我们模型中大气中碳质量（\(cM_a\)）随PETM异常时间（\(t_{\text{PETM}}\)）的变化。数值来自我们的放松模型（方程11），取 \(cM_{\text{ab}} = 1400 \, \text{Gt}\)，\(cM_{a0} = 3050 \, \text{Gt}\)，\(t_u = 100 \, \text{kyr}\)。