An Overview of Aerosol-Cloud Interactions

Hamish Gordon1, Franziska Glassmeier2, and Daniel T. McCoy3

Clouds and Their Climatic Impacts: Radiation, Circulation, and Precipitation, Geophysical Monograph 281, First Edition.

Edited by Sylvia C. Sullivan and Corinna Hoose.

摘要

气溶胶-云相互作用指的是一组大气过程，通过这些过程气溶胶影响云的性质，有时云也会影响气溶胶。这些大气过程对地球辐射平衡的影响可能很大，但存在不确定性。由于气溶胶浓度的不确定性来源于排放和气溶胶过程，因此气溶胶-云相互作用的不确定性主导了我们对地球气候辐射强迫知识的整体不确定性。气溶胶主要通过改变云凝结核和冰核的数量（即“间接效应”）来影响云， 有时还通过影响云的温度（即“半直接效应”）。云过程因气溶胶-云相互作用而发生变化，可能导致云的大气物理特性，如覆盖范围和凝结物量，发生显著调整。气溶胶-云相互作用的研究主要通过分析观测数据、进行实验室实验和构建模型来模拟气溶胶如何影响云，以便更好地理解相关的大气过程。本综述概述了相关的大气科学，并重点介绍了最近应用于更好理解气溶胶-云相互作用及其对辐射平衡影响的一些有前景的技术，例如高斯过程模拟。本章节旨在为本书系列后续章节提供背景，并作为研究生介绍气溶胶-云相互作用领域当前研究的入门。

引言与动机

气溶胶对云的形成具有基础性的重要性。 在没有气溶胶的情况下，空气中的相对湿度必须达到420%才能使水蒸气在离子等适宜表面上凝结（Mason, 1960；Wilson, 1900）。 这种高饱和度的情况在地表附近不太可能发生，因为水会凝结为露水。因此，如果没有气溶胶，雾和边界层云将可能极为稀少或完全不存在。 相反，如果没有云，大气中的气溶胶状况也会完全不同，可能以显著更高的浓度存在。

气溶胶-云相互作用对气候的重要性

气候相关的关键问题是，气溶胶对自然背景浓度的扰动会对云产生多大的影响。 改变能够充当云凝结核（CCN）的气溶胶数量，会导致云滴浓度的变化，从而改变云的反射率或反照率（albedo）。 当这种效应与由气溶胶浓度变化引起的云凝结量（液态或冰态混合比）的变化分开考虑时，被称为Twomey效应（Twomey, 1974, 1977）。 除了反照率，云滴浓度的扰动还会影响云中的微观过程，包括碰撞-聚结形成暖雨（Albrecht效应，Albrecht, 1989）、过饱和水蒸气的凝结、云滴的沉降速度以及单个云滴的蒸发时间。 此外，改变能够作为冰核的气溶胶数量（即水可冻结的表面）同样会影响云的辐射特性和降水概率。

通过这些过程，气溶胶对云反照率和微观特性的影响被称为气溶胶对地球辐射平衡的间接效应。这些效应与气溶胶直接对辐射的散射和吸收作用以及由气溶胶吸收引起的云附近热力学扰动（称为半直接效应，Hanse et al., 1997）相区分。

气溶胶-云相互作用（简称ACI）对长期辐射平衡的最显著影响，可以通过考虑气溶胶的自然背景浓度（如前工业时代的大气）与其工业化以来的扰动总量来体现。 人为气溶胶增加了地球反射辐射的量，抵消了工业时期二氧化碳浓度增加引起的20%到50%的变暖（Bellouin et al., 2020；Charlson et al., 1992；Twomey et al., 1984）。 这一气溶胶效应的大部分归因于气溶胶通过ACI对气候的间接强迫，而非气溶胶自身的直接辐射效应。由于Twomey效应随时间增强导致的地球气候辐射强迫通常缩写为RFaci。 如果还包括因气溶胶驱动的云微物理特性变化导致的云宏观特性（如面积、厚度）调整，则产生的辐射强迫称为“有效辐射强迫”（ERFaci）。

Bellouin等（2020）估计ERFaci的不确定性范围在-1.73到-0.27 W/m²之间（16%-84%区间）。这种不确定性是大气科学界持续努力理解ACI的主要动机。 Hansen等（2011）直言不讳地指出，“气溶胶的不确定性是定量理解气候变化的主要障碍。”因此，ACI在研究云在气候系统中作用时至关重要。

此外，ACI对气候还有许多更微妙的影响，例如涉及若干重要反馈回路（Gettelman et al., 2016）以及对大气环流的作用（例如，Mann et al., 2018；Wilcox et al., 2020）。随着气候变暖，大气中云覆盖和厚度的变化可能会受到气溶胶浓度变化的影响，从而进一步显著改变未来气候中的ERFaci。

本综述的提纲与目标

气溶胶-云相互作用（ACI）已成为许多近期综述文章的主题（Bellouin等，2020；Fan等，2016；Kreidenweis等，2019；Mülmenstädt等，2018；Rosenfeld等，2014；Seinfeld等，2016；Storelvmo，2017；Tao等，2012），我们也知道其他综述文章正在准备中。

本篇贡献是有选择性的，而非全面性的，旨在补充这些不同的观点。我们提供了一个简短的介绍性概述，旨在为本书后续章节提供背景，并跟进当前研究中的一些新兴趋势。

我们首先简要概述了在不同气象条件下感兴趣的ACI。接下来，我们详细讨论了几个关键的暖云过程：气溶胶的激活、雨水形成过程以及反照率。

然后，我们概述了一些新的方法论，旨在理清气溶胶-云相互作用。接下来是关于冷云的讨论，最后讨论田间实验和卫星观测。为了使综述保持合理长度，我们并未讨论云如何影响气溶胶，尽管我们承认这种效应也可能对地球气候产生反馈和影响，如Carslaw等（2010）和Tegen与Schepanski（2018）所讨论的。

气溶胶如何影响不同类型的云

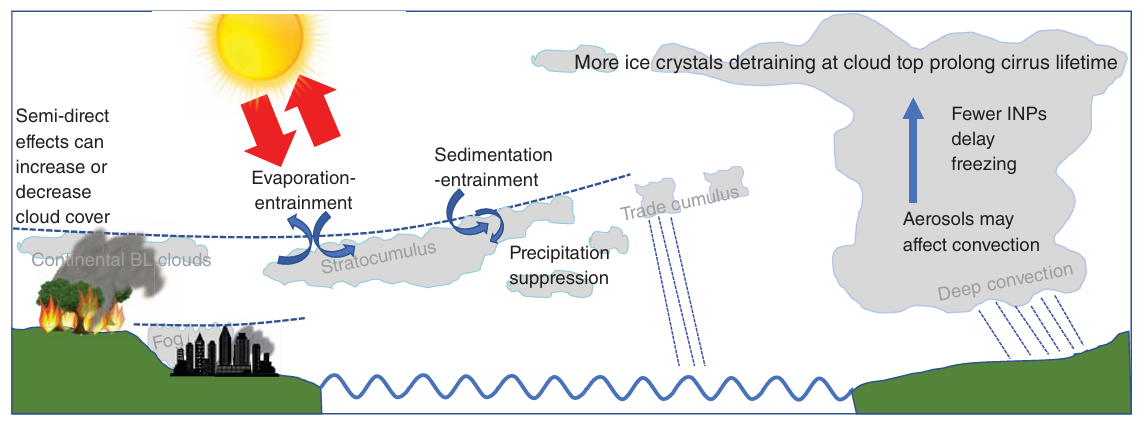
气溶胶-云相互作用根据发生的气象条件的不同而有很大差异。图2.1展示了一些不同的气象条件。

暖云是指不含冰且温度不低于0°C的云；我们注意到，过冷液态云不是暖云。在热带和中纬度的暖非降水低云（层云和层积云）及雾中，对于给定的液态水含量（LWC），云滴的大小取决于云滴的数量浓度。 这种依赖性反过来导致云滴浓度增加对云反照率（RFaci）的显著且相对较为明确的影响。其他可能的ACI包括蒸发-夹带和沉降-夹带反馈（Hill等，2009），这些内容也将在第12章《云与环境的小尺度混合》讨论。 首先，蒸发-夹带反馈的情况是，较高的云滴浓度会导致云滴的沉降速度减慢。Ackerman等（2004）表明，沉降速度减慢会增加干空气的夹带，导致更多云滴蒸发，从而减少云的反照率和水含量。Bretherton等（2007）发现，这种增加的夹带是由于沉降速度较慢时，更多云水被集中到云顶。因此，云顶的蒸发速率随着LWC的增加而增加，夹带效应则通过蒸发冷却得到增强。此外，较小的云滴蒸发更快，促进了更多的湍流，并增加了干空气的夹带：即蒸发-夹带反馈（Homann & Feingold, 2019；Small等，2009；Wang等，2003）。

在低气溶胶浓度的暖雨云中，另一个可能变得重要的ACI是Albrecht效应（Albrecht，1989）。这种气溶胶和降水的现象常见于远洋大气。近期研究表明，Albrecht效应在非常干净的云中最为显著，甚至可能仅在云滴浓度低于约30cm−3的云中发生，尽管这一阈值存在很大不确定性。当气溶胶浓度如此低时，云滴较大，因此，云滴需要较少的碰撞-聚结事件才能长成细雨或雨滴。相反，在污染环境中，细雨会被抑制。 这一机制也可能在云滴浓度较高时减缓降水过程，例如在山地云中（Givati & Rosenfeld, 2004）。然而，一些在非常大的可溶气溶胶上核化的云滴，称为巨型云凝结核，会由于其高溶质浓度（Johnson, 1982）而有效地长成雨滴（Jensen & Nugent, 2017）。 增加这些大气溶胶的浓度应当在某一程度上加速降水的开始，并减少云液水路径（LWP）（Posselt & Lohmann, 2008）。

热带信风积云（第7章《热带海洋低云》）以及拥塞云和深对流云通常具有较高的垂直速度（大于1.0m/s）。在这些云中，大气溶胶的浓度通常较低（积聚模式中低于200cm−3），因为这些气溶胶通常会被降水清除。因此，与其他类型的云相比，过饱和度可能会达到更高的值，并且较小的气溶胶可能会被激活为云滴。 几位作者探讨了气溶胶浓度与云中凝结和冻结过程中潜热释放的幅度和高度之间的可能联系，并进一步研究气溶胶是否能影响深层云中的液态与冰态凝结的相对比例。有关气溶胶对深层云的影响将在第2.7节进一步讨论。简而言之，在更为污染的云中，理论上气溶胶的较大表面积应导致比干净云层在更低的高度进行更多的凝结。凝结的低高度和随之而来的潜热释放会影响上升气流速度，但关于这些潜热加热效应的强度，学术界并未达成一致（Fan等，2007；Grabowski & Morrison, 2016, 2020）。

在混合相云中（如在气旋和热带深对流云中），除了由于潜热加热导致的增强效应外（Fan等，2018；Khain等，2004），高云滴浓度还可能抑制或促进云滴冻结（Pruppacher & Klett, 2010；Yin等，2005）。 延迟的暖雨形成可能会增强后来的冷雨（Rosenfeld等，2008），并改变云顶的辐射特性。如果云滴均匀冻结，则更多的云滴会直接转化为更多的冰晶；而如果它们是异质冻结的，则冰晶浓度更多依赖于冰核的浓度，以及一些尚未完全理解的冰晶增生过程。 较大的冰晶具有显著更高的沉降速率，因此，气溶胶也会影响卷云（Kärcher & Lohmann, 2003）和高纬度地区的混合相云的寿命。

气溶胶激活

除了半直接效应外，所有气溶胶-云相互作用（ACI）都依赖于气溶胶对云滴浓度的影响。 在所有暖云中，可能在大多数冷云中，液态云滴浓度的主要来源是气溶胶激活，激活速率由冷却速率（通常是由空气上升运动引起的）、气溶胶浓度和属性以及温度决定。 云滴的蒸发、云滴的冻结、暖雨形成和霜冻是气溶胶激活的“汇”。Bellouin等（2020）估计，从1850年到2005-2015年期间，云滴浓度增加了5%到17%。 当水蒸气的过饱和度超过该颗粒的临界过饱和度（Sc）时，气溶胶粒子就会激活为云滴。过饱和度通常是由空气上升时冷却引起的。

\[ Sc = \left( \frac{4A^3}{27\kappa r_d^3} \right)^{1/2} \quad (2.1) \]

其中，A是表面张力与温度之比，\(\kappa\)是体积加权的吸湿性，\(r_d\)是气溶胶的干半径（Ghan等，2011）。

因此，对于给定的气溶胶粒子，临界过饱和度主要取决于其大小（Dusek等，2006），还与吸湿性（Köhler，1936；Petters & Kreidenweis，2007）和表面张力（Prisle等，2012；Shulman等，1996）有关。 较大、吸湿性强、表面张力低的颗粒在较低的过饱和度下就能激活，而较小、吸湿性差、表面张力高的颗粒则需要较高的过饱和度才能激活，分子表面-体积分配，尤其是表面活性剂的分布，在确定表面张力和吸湿性方面也起着重要作用（Petters & Kreidenweis，2013；Sullivan等，2009）。 吸湿性对激活的依赖性、硫酸对新气溶胶形成的关键作用以及大规模的硫化合物人类排放共同解释了为何气溶胶-云相互作用对气候的辐射强迫更依赖于硫酸盐，而非其他气溶胶物种（Boucher & Lohmann，1995；Charlson等，1992）。 要计算临界过饱和度是否被超过，需要考虑气溶胶粒子的数量，因为气溶胶会在激活之前吸湿。如果云滴已经存在，也应考虑进去。 在暖云中，远高于云基的地方（激活较不可能发生），云滴而非气溶胶通常主导水蒸气的汇。过饱和度S的计算公式为：

\[ S = \left( \frac{w}{2\pi G} \frac{d q_l}{dz} \right)^{1/3} \left( \frac{1}{N_d^2} q_l \right) \quad (2.2) \]

其中，w是垂直空气速度，G是增长因子，主要依赖于温度，\(q_l\)是液态水含量（LWC），z是高度，\(N_d\)是云滴浓度（Yang等，2019）。

类似的方程（Korolev & Mazin，2003；Politovich & Cooper，1988；Squires，1952）不需要知道\(\frac{d q_l}{dz}\)，但依赖于假设过饱和度源、上升气流和水蒸气到云滴的汇之间的准稳态。

即使在云基，也可以很好地近似这一假设，前提是正确考虑了垂直速度的湍流波动（Prabhakaran等，2020）。然而，通常在云基使用更复杂的参数化方法来考虑水蒸气对气溶胶的汇（Ghan等，2011；Twomey，1959）；其中最常用的是Abdul-Razzak和Ghan（2000）的方法，它采用了Köhler（1936）的框架。

更详细的模型，通常具有粒度解析的云微物理过程，能够在不使用“饱和调整”近似的情况下处理激活过程，通常天气和气候模型会采用这一近似（Khain等，2000）。

该近似假设水蒸气在每个时间步结束时迅速凝结到云滴或冰晶上，从而使过饱和度降为零，在此时水蒸气和凝结物达到平衡。没有这一假设的详细模型必须“预报”过饱和度，这意味着它们必须跟踪过饱和度从一个时间步到下一个时间步的演变。

这些模型在现有云中激活过程较为重要时尤其需要（Fridlind等，2004），并且可能也适用于雾（Schwenkel & Maronga，2019；Thouron等，2012）。

在雾中，过饱和度可能由辐射冷却生成，而非由上升气流速度引起。

然而，最近已有一些方法被开发出来，可以使得在雾中或云基上方的激活过程能够在较大尺度的天气和气候模型中进行近似（Gordon等，2020；Poku等，2021；Wang等，2013；Yang等，2015）。

气溶胶的粒径分布（Kulkarni & Wang，2006；Liu等，1974；Wang & Flagan，1989）以及在不同水蒸气过饱和度下的云凝结核（CCN）浓度（Chuang等，2000；Hudson & Squires，1976）可以通过机载现场仪器准确测量，云滴的粒径分布（Baumgardner等，2001；Knollenberg，1976）和上升气流速度（Axford，1968；Wood等，1997）也可以准确测量。

然而，气溶胶激活的完美闭合研究仍然难以实现，主要是因为云滴的核化并不总是发生在与它们被检测到相同的地方或相同的时间。

激活过程可以通过像密歇根理工大学的Pi腔室（Prabhakaran等，2020；Shaw等，2020）这样的实验室实验来更好地观察。

这种云物理研究技术经受住了时间的考验（Aitken，1881），并且仍然为未来更多定量研究气流与微物理之间的关键相互作用提供了巨大潜力。

暖云反照率

在前面的章节中，我们描述了气溶胶如何激活为云滴。在这里，我们描述了气溶胶通过控制云滴数浓度（Nd）如何直接影响云的反照率（𝛼）。通过改变云滴的数量浓度，气溶胶对云反照率的改变，独立于任何云凝结量的变化，被称为第一间接效应或Twomey效应（Twomey，1977）。

基于Lorenz-Mie理论，云的光学厚度（𝜏）是液态云滴集合体的消光截面，其几何半径为（r），云滴的尺寸分布为（nd(r)）。其表达式为：

\[ \tau = \int_0^h \int_0^\infty Q_e \pi r^2 n_d(r) \, dr \, dz \quad (2.3) \]

其中，Qe是消光效率，z是垂直距离，h是几何云高，Qe≈2对于液态云滴。有效半径（re）与散射面积成比例，其公式为：

\[ r_e = \frac{\int_0^\infty r \pi r^2 n_d(r) \, dr}{\int_0^\infty \pi r^2 n_d(r) \, dr} \quad (2.4) \]

云内某一体积的液态水含量（LWC）为：

\[ LWC = \frac{4\pi}{3} \rho_{liq} \int_0^\infty r^3 n_d(r) \, dr \quad (2.5) \]

将方程（2.5）除以方程（2.3）中的积分项，并假设Qe≈2，重新排列并对高度积分，得到：

\[ \tau = \int_0^h \frac{3}{2 \rho_{liq}} \frac{LWC(z)}{r_e(z)} \, dz \quad (2.6) \]

按照S. Twomey（1977）原始的表述方式，我们希望将其表示为云滴数量浓度Nd的函数。这是有用的，因为Nd主要取决于云凝结核（CCN）的数量浓度，且与有效半径（re）相比，Nd在第一近似下与LWC无关。Nd是LWC除以云滴质量，公式为：

\[ N_d(z) = LWC(z) \cdot \left( \frac{\rho_{liq}}{4\pi r(z)^3 3} \right)^{-1} \quad (2.7) \]

为了从卫星数据中计算Nd，插入一个常数因子k = \( \frac{r^3}{r_e^3} \) 允许使用有效半径而不是实际半径来计算。测量从太空中获得的Nd时，还必须考虑云的亚绝热程度（fad）。我们可以将云的LWC表示为绝热性和云的垂直扩展的函数：

\[ LWC(z) = f_{ad} \Gamma_{ad} z \quad (2.8) \]

其中，Γad是LWC随高度增加的绝热率，它是压力和温度的函数。使用方程（2.8）和（2.7）代入方程（2.6），我们可以将云的光学厚度表示为Nd、云的几何深度和绝热性的函数：

\[ \tau = A \cdot \left( f_{ad} \Gamma_{ad} \right)^{2/3} N_d^{1/3} h^{5/3} \quad (2.9) \]

其中A是常数，等于 \( \left( \frac{243\pi}{250 \rho_{liq}^2} \right)^{1/3} \)。因此，云的光学厚度是Nd的弱函数。它也可以用LWP而不是云厚度来表示，通过方程（2.8）的积分版本：

\[ \tau = N_d^{1/3} \cdot LWP^{5/6} \cdot A \cdot \left( \frac{32}{f_{ad} \Gamma_{ad}} \right)^{1/6} \quad (2.10) \]

增加Nd会增加云的光学厚度，并产生第一个间接效应，即气溶胶-云辐射效应。云反照率或反射率（𝛼）与Nd的依赖关系进一步减弱：假设保守散射允许我们近似为（Lacis & Hansen，1974）：

\[ \alpha \sim \frac{\tau}{\tau + \eta} \quad (2.11) \]

其中𝜂是常数，根据非对称性参数（通常用符号g表示）的值以及在推导方程时的假设而变化。非对称性参数是散射角余弦的强度加权平均值。对于典型的g值为0.85时，𝜂的范围是7（Petty，2006）到13.3（Tornow等，2020）。

公式的10/3次方中，Nd的变化以及𝛼与𝜏之间的关系显示，在高Nd时，增加Nd的效应会减小。其后果之一是前工业状态在决定ERFaci时的重要性（Carslaw等，2013）。

𝜏与Nd的依赖关系以及𝛼与𝜏的关系在图2.2中有所展示。

气溶胶引起的云反照率变化会转化为大气顶层辐射平衡的变化：

\[ dR = d \left( R_{in}^{SW} [A_{cldc} + (1 - c) A_{clr}] - R_{out}^{LW} \right) \quad (2.12) \]

其中，Rin^SW表示入射短波辐射，Rout^LW表示出射长波辐射，c为云量，Aclr/cld为大气顶层的晴空和云空反照率。长波部分可以忽略，除非气溶胶变化影响到云顶温度，或者云层较薄（例如Garrett等，2002年2月1日）。

此外，Rin^SW的变化通常也可以忽略，至少在亚十年时间尺度上。Diamond等（2020）提供了一个食谱来将辐射平衡变化与部分云覆盖下的反照率相关联，考虑了大气层以上云层的透射率和反照率。在污染较少的海洋地区，当地表反照率和大气反照率较小，且云量变化不大时，方程（2.12）可以近似为：

\[ dR \propto d(\alpha \cdot c) \quad (2.13) \]

其中𝛼是云反照率。然而，在陆地或海冰上，在污染条件下，或者对于高云或厚云（因为近似假设大气反照率与晴空反照率相似），方程（2.13）不再有效。

确定灵敏度的方法

气溶胶对云辐射特性的影响可以通过将场景反照率变化

$$ dR = d(\alpha \cdot c) $$

(方程 2.13) 与导致场景反照率变化的云滴浓度扰动 \(dN_d\) 相关联来量化：

$$ \frac{d \ln R}{d \ln N_d} = \frac{d \ln \alpha}{d \ln N_d} + \frac{d \ln c}{d \ln N_d}, $$

(方程 2.14)。其中，引入对数导数

$$ \frac{d \ln R}{d \ln N_d} = \frac{(dR / R)}{(dN_d / N_d)} $$

作为方便的标记，并按照 Platnick 和 Twomey (1994) 的方法广泛称为灵敏度。

假设云滴数浓度的扰动是由于气溶胶数浓度的变化 \(dN_a\) 引起的，而不是由降水或云内热力变化引起的。其数值对应于 \(R\) 对 \(N_d\) 的 1% 变化所产生的百分比变化。

将云反照率表示为 \(N_d\) 的嵌套函数：

$$ \alpha = \alpha\{\tau[N_d, \text{LWP}(N_d)]\}, $$

其中，\(\alpha(\tau)\) 由方程 (2.11) 给出，而 \(\tau(N_d, \text{LWP})\) 由方程 (2.10) 给出。应用链式法则可对暖云提供以下简化：

$$ \frac{d \ln \alpha}{d \ln N_d} = \frac{\partial \ln \alpha}{\partial \ln \tau} \cdot \frac{d \ln \tau}{d \ln N_d} = \frac{\partial \ln \alpha}{\partial \ln \tau} \left( \frac{\partial \ln \tau}{\partial \ln N_d} + \frac{\partial \ln \tau}{\partial \ln \text{LWP}} \cdot \frac{d \ln \text{LWP}}{d \ln N_d} \right) $$

$$ = (1 - \alpha) \left( \frac{1}{3} + \frac{5}{6} \cdot \frac{d \ln \text{LWP}}{d \ln N_d} \right). $$

请注意，偏导数 (符号：\(\partial\)) 量化了相对于一个特定变量的变化，同时将其他所有变量保持固定。类似方程 (2.10) 的幂函数的偏对数导数对应于其指数，因此与任何常数预因子无关。

总结方程 (2.14) 和 (2.16)，得到部分云场景的总体灵敏度 (Bellouin et al., 2020)：

$$ \frac{d \ln R}{d \ln N_d} = \frac{1 - \alpha}{3} + \frac{5(1 - \alpha)}{6} \cdot \frac{d \ln \text{LWP}}{d \ln N_d} + \frac{d \ln c}{d \ln N_d}. $$

$$ = \frac{\partial \ln R}{\partial \ln N_d} + \frac{\partial \ln R}{\partial \ln \text{LWP}} \cdot \frac{d \ln \text{LWP}}{d \ln N_d} + \frac{\partial \ln R}{\partial \ln c} \cdot \frac{d \ln c}{d \ln N_d}. $$

其中，第一等式(如方程 2.16) 严格适用于暖云。第二等式假设更普遍适合基于函数关系 \(R = f(N_d, \text{LWP}, c)\) 量化 \(R\) 的变异性。

线性回归的局限性

传统上，对数导数通过对数空间中的线性回归斜率进行经验量化。

线性回归进一步假设量与量之间具有恒定指数的幂律关系。然而，这种关系可能仅在某些条件下作为有效近似。

灵敏度的时间依赖性

最后，\(\text{LWP}\) 对 \(\text{N}_d\) 的响应可能不是瞬时的，而是随时间演变，从而使灵敏度具有时间依赖性 (Glassmeier et al., 2021)。